When creating software, it is useful to consider the efficiency of an algorithm. Two of the main measures of efficiency for an algorithm are time complexity and space complexity. Time complexity is defined as the time taken for an algorithm as a function of the input size and space complexity is defined as the amount of memory space being required. Often but not exclusively time complexity and space complexity can be expressed using Big O notation that usually considers the worst case.
Why Complexity Matters?
Higher efficiency algorithms ensure lower execution time and resource consumption, particularly for huge datasets. A proper algorithm will weigh heavily on the application’s performance and scalability.
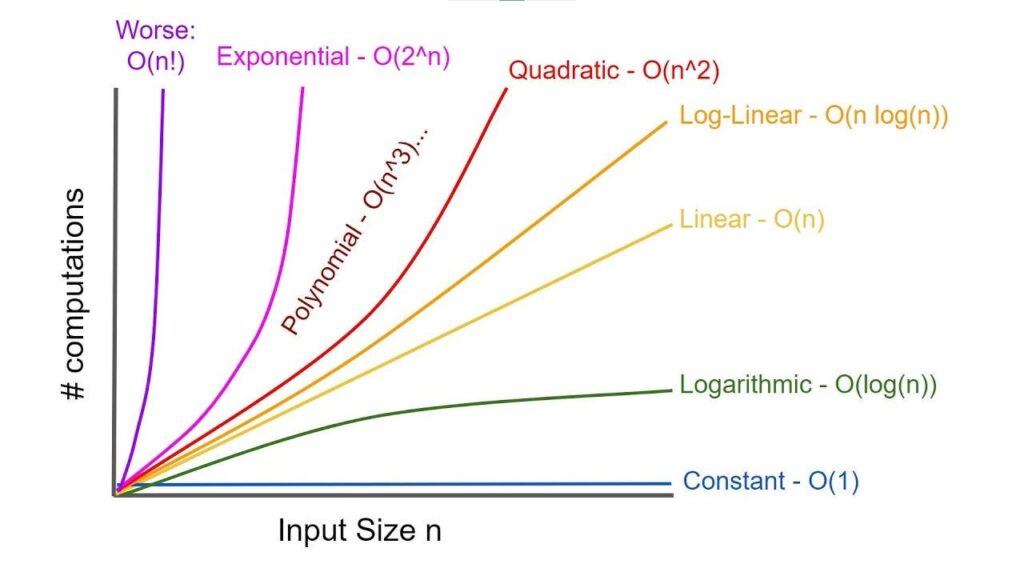
1. Time Complexity:-
Time Complexity Classes
- O(1) – Constant Time: Execution time remains constant regardless of input size.
- O(log n) – Logarithmic Time: Execution time grows logarithmically, typical in divide and conquer algorithms like binary search.
- O(n) – Linear Time: Execution time grows linearly with input size, common in simple loops.
- O(n log n) – Quasilinear Time: Execution time grows proportionally to n times log n, seen in efficient sorting algorithms like Merge Sort and Quick Sort (average case).
- O(n²) – Quadratic Time: Execution time grows quadratically, often due to nested loops (e.g., Bubble Sort).
Time complexity of different algorithms:
Algorithms
a. Linear Search
b. Binary Search
c. Bubble Sort
d. Selection Sort
e. Insertion Sort
f. Merge Sort
g. Quick Sort
h. Heap Sort
i. Bucket Sort
j. Radix Sort
k. Tim Sort
l. Shell Sort
Average Time Complexity
O(n)
O(log n)
O(n²)
O(n²)
O(n²)
O(n log n)
O(n log n)
O(n log n)
O(n + k)
O(n k)
O(n log n)
O((n log (n))^2)
Best Time Complexity
O(1)
O(1)
O(n)
O(n²)
O(n)
O(n log n)
O(n log n)
O(n log n)
O(n + k)
O(n k)
O(n)
O(n)
Worst Time Complexity
O(n)
O(log n)
O(n²)
O(n²)
O(n²)
O(n log n)
O(n²)
O(n log n)
O(n²)
O(n k)
O(n log n)
O((n log (n))^2)
Best Time Complexity:
Algorithms
a. Linear Search
b. Binary Search
c. Bubble Sort
d. Selection Sort
e. Insertion Sort
f. Merge Sort
g. Quick Sort
h. Heap Sort
i. Bucket Sort
j. Radix Sort
k. Tim Sort
l. Shell Sort
Best Case
O(1)
O(1)
O(n)
O(n²)
O(n)
O(n log n)
O(n log n)
O(n log n)
O(n + k)
O(n k)
O(n)
O(n)
Avg. Time Complexity:-
Algorithms
a. Linear Search
b. Binary Search
c. Bubble Sort
d. Selection Sort
e. Insertion Sort
f. Merge Sort
g. Quick Sort
h. Heap Sort
i. Bucket Sort
j. Radix Sort
k. Tim Sort
l. Shell Sort
Avg. Case
O(n)
O(log n)
O(n²)
O(n²)
O(n²)
O(n log n)
O(n log n)
O(n log n)
O(n + k)
O(n k)
O(n log n)
O((n log (n))^2)
Worst Time Complexity:-
Algorithms
a. Linear Search
b. Binary Search
c. Bubble Sort
d. Selection Sort
e. Insertion Sort
f. Merge Sort
g. Quick Sort
h. Heap Sort
i. Bucket Sort
j. Radix Sort
k. Tim Sort
l. Shell Sort
Worst Case
O(n)
O(log n)
O(n²)
O(n²)
O(n²)
O(n log n)
O(n²)
O(n log n)
O(n²)
O(n k)
O(n log n)
O((n log (n))^2)
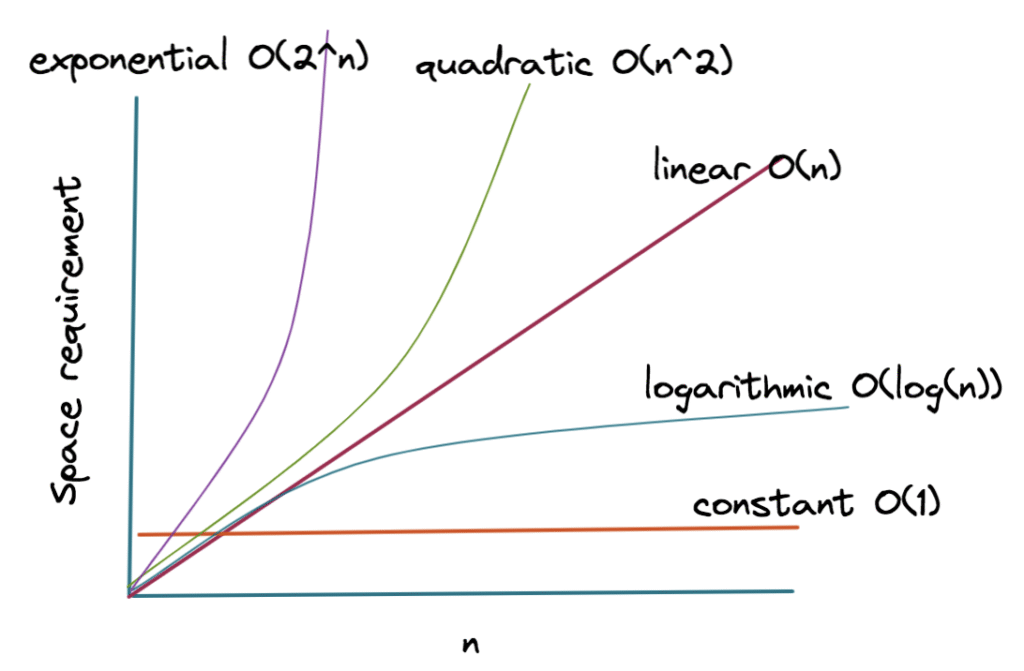
2. Space Complexity:
Space Complexity Classes
- O(1) – Constant Space: Memory usage remains constant regardless of input size; in place algorithms typically fall here.
- O(log n) – Logarithmic Space: Memory usage grows logarithmically, often due to recursion depth in divide and conquer algorithms.
- O(n) – Linear Space: Memory usage grows linearly with input size; common when creating auxiliary data structures proportional to input.
- O(n²) – Quadratic Space: Memory usage grows quadratically, such as when storing all pairs in a matrix or graph adjacency matrix.
Space complexity of different algorithms:
Algorithms
a. Linear Search
b. Binary Search
c. Bubble
Sort
d. Selection Sort
e. Insertion Sort
f. Merge
Sort
g. Quick
Sort
h. Heap
Sort
i. Bucket
Sort
j. Radix
Sort
k. Tim
Sort
l. Shell
Sort
Worst Case
O(1)
O(1)
O(1)
O(1)
O(1)
O(n)
O(log n)
O(n)
O(n)
O(n + k)
O(n)
O(1)
Algorithms
a. Linear Search
b. Binary Search
c. Bubble Sort
d. Selection Sort
e. Insertion Sort
f. Merge Sort
g. Quick Sort
h. Heap Sort
i. Bucket Sort
j. Radix Sort
k. Tim Sort
l. Shell Sort
Worst Space Complexity
O(1)
O(1)
O(1)
O(1)
O(1)
O(n)
O(log n)
O(n)
O(n)
O(n + k)
O(n)
O(1)
Conclusion:-
Analyzing space complexity is crucial for developing memory efficient algorithms. By understanding how memory usage scales with input size, developers can make informed decisions to optimize their code and prevent excessive memory consumption.
